Ratio de Sharpe définition

Le ratio de Sharpe est une formule de calculs permettant d’apprécier le rendement d’un investissement en comparaison de sa volatilité.

Ce ratio est un moyen d’ajuster le rendement d’un actif ou d’un portefeuille au risque qu’il encourt.

Cette formule fut élaborée par le prix Nobel d’économie William F. Sharpe. Il est par ailleurs connu pour avoir conçu le modèle d’évaluation des actifs financiers – MEDAF (Capital Asset Price Model – CAPM), largement utilisé dans la gestion classique de portefeuilles.

Sommaire :

• Ratio de Sharpe définition
• Comment interpréter le ratio de Sharpe ?
• Les limites du ratio de Sharpe
• Le ratio de Sortino comme mesure alternative

Ratio de Sharpe définition

Le ratio de Sharpe a été créé en 1966 par William Sharpe, un éminent économiste américain. Il est toujours très utilisé de nos jours afin de déterminé si un investissement est suffisamment intéressant. Autrement dit, il permet d’évaluer le potentiel de ROI (Retour Sur Investissement) d’un actif.

La formule du ratio de Sharpe se définit de la manière suivante :

S = (R_p – R_f) / σ_p

Avec :

• R_p : le rendement d’un actif (action ou crypto par exemple) ou d’un portefeuille.
• R_f : le rendement de l’actif « sans risque ». De manière traditionnelle, les obligations d’État d’un pays développé. Le plus souvent les bons du Trésor américain servent de point de référence.
• σ_p : l’écart-type extrêmes des rendements passés de l’actif examiné ; aussi nommé sa déviation standard.

En d’autres mots, le ratio de Sharpe soustrait le rendement d’un actif sûr au rendement du portefeuille évalué. Ce résultat est ensuite divisé par une mesure de la volatilité de ce portefeuille.

De la sorte, plus l’actif ou le portefeuille examiné est volatile, plus le dénominateur de la formule est grand, et plus le ratio de Sharpe sera faible. Donc, toute chose égale par ailleurs, moins le portefeuille sera intéressant.

Ainsi, à rendements identiques, le portefeuille le plus avantageux est celui qui présente la plus faible volatilité, donc, en théorie, le risque le plus faible.

De façon plus précise, si le ratio de Sharpe est compris entre 0 et 1, cela signifie que le risque encouru, mesuré par sa volatilité du portefeuille, n’en vaut pas l’intérêt. Autrement dit qu’un portefeuille moins risqué pourrait apporter le même rendement, ou inversement qu’un portefeuille exposé à la même volatilité pourrait apporter des rendements supérieurs.

Un bon portefeuille ne saurait donc afficher un ratio de Sharpe inférieur à 1.

Comment interpréter le ratio de Sharpe ?

Interpréter le ratio de Sharpe revient à comparer les performances de fonds d’investissement. Il peut aussi être utile afin d’évaluer l’opportunité d’allouer de nouveaux capitaux à un portefeuille, au cas où les nouveaux fonds affecteraient la performance du portefeuille.

Il met en relation le lien entre le rendement et la volatilité comme risque de l’investissement.

À lire aussi :

Couple rendement risque : comment trouver le bon équilibre ?

Supposons par exemple qu’un client potentiel souhaite choisir entre deux portefeuilles d’investissement, dans un environnement financier offrant un taux « sans risque » de 2 %.

Le portefeuille A offre un rendement moyen de 16 % pour un écart-type de 12 %.

Son ratio de Sharpe est obtenu par le calcul suivant : (16 – 2) / 12 = 1,17

Le portefeuille B offre, quant à lui, un rendement moyen de 12 % pour un écart-type de 7 %.

Cette fois-ci, le ratio de Sharpe atteint : (12 – 2) / 7 = 1,43

Le second portefeuille offre un rendement brut inférieur. Toutefois, ajusté à la volatilité encourue par le passé, ce portefeuille est plus avantageux car son ratio de Sharpe est plus élevé. Il est donc préférable d’opter pour le portefeuille B, car sa composition est plus efficiente.

Si l’on désire cependant obtenir un rendement de 16 % et non seulement de 12 %, il suffira d’employer un effet de levier approprié avec le portefeuille B plutôt que d’opter pour le portefeuille A.

De la sorte, le ratio de Sharpe plus élevé du second portefeuille ne sera pas affecté. Il restera donc supérieur au premier portefeuille, car la volatilité et les rendements du portefeuille s’élèveront dans la même proportion.

Les limites du ratio de Sharpe

Toutefois, le risque encouru par un portefeuille ne se confond pas, en pratique, avec sa volatilité.

En particulier, la volatilité à la hausse n’est en aucun cas un risque, mais tout au contraire une qualité recherchée par l’investisseur. Seule la volatilité à la baisse lui est préjudiciable.

À cela, s’ajoute la supposition que les performances passées sont un indicateur valable pour les performances à venir. Or le monde de la finance connaît beaucoup d’exemples qui prouvent le contraire.

En outre, le ratio de Sharpe peut être manipulé. De longs intervalles de mesures présentent des variations moins volatiles en terme de pourcentage que de brefs intervalles.

Ainsi, les variations hebdomadaires présentent des écarts-types moins étendus que les variations quotidiennes. De plus, l’étendue de la période passée à prendre en compte peut également être « ajustée ». Ceci afin d’éviter de prendre en compte les moments de volatilité extrême.

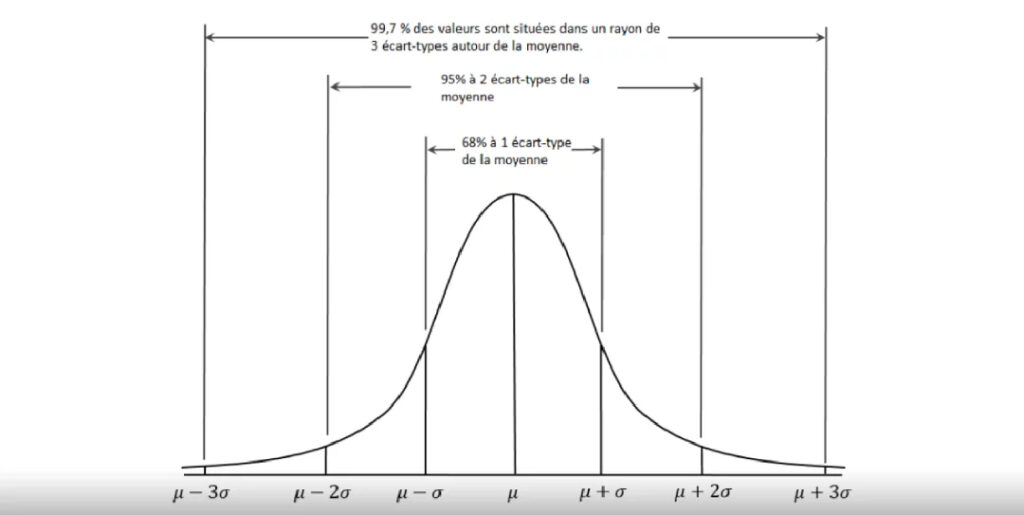
De plus, la mesure de l’écart-type des rendements d’un portefeuille suppose que sa distribution de valeurs est normale. Cela signifie qu’elle forme une courbe en cloche : les variations jusqu’aux extrêmes seraient ainsi, en théorie, rares.

Or les fluctuations des cours boursiers, en particulier pour des actifs individuels, peuvent tout à fait présenter une distribution différente, bien loin d’une courbe en cloche.

Enfin, le ratio de Sharpe ne permet pas de se prémunir des actifs frauduleux, notamment des projets bâtis sur un Schéma de Ponzi. Ces derniers peuvent présenter des ratios de Sharpe très élevés pour attirer les investisseurs. Pour autant, ils ne reflètent pas la réalité puisque les données d’entrées sont fausses.

C’est pourquoi le ratio de Sharpe ne peut être utilisé seul comme indicateur fiable d’un investissement intéressant. Il est nécessaire de creuser plus en profondeur sur les caractéristiques de l’actif et de recourir à des outils complémentaires pour s’assurer d’obtenir un ROI valable.

Le ratio de Sortino comme mesure alternative

Afin de pallier les insuffisances du ratio de Sharpe, et en particulier sa définition implicite de la volatilité à la hausse comme un risque, Frank A. Sortino développa un ratio qui porte aujourd’hui son nom.

Le ratio de Sortino est ainsi une variation du ratio de Sharpe, substituant seulement à la déviation standard de rendements extrêmes à la hausse comme à la baisse, la déviation standard des rendements les plus faibles.

Par ce moyen, seule la volatilité préjudiciable à l’investisseur est prise en compte, et non la volatilité haussière qui, elle, est bien entendu positive.

La formule du ratio de Sortino est la suivante :

S = (R_p – R_f) / VB_p

Avec les éléments suivants :

• R_p : le rendement d’un actif ou d’un portefeuille.
• R_f : le rendement de l’actif « sans risque ». De manière traditionnelle, les obligations d’État d’un pays développé. Le plus souvent les bons du Trésor américain servent de point de référence.
• VB_p : la volatilé négative (à la baisse) de l’actif.

Une seconde mesure alternative au ratio de Sharpe est le ratio de Treynor. Cet indicateur consiste à placer au dénominateur le bêta du portefeuille examiné.

Il se calcul de la manière suivante :

T = (R_p – R_f) / β_p

Où :

• R_p égale la rentabilité passée du portefeuille ou de l’actif
• R_f correspond au rendement d’un actif « sans risque » (exemple : Obligation d’Etat)
• β_p est une mesure du risque systémique d’un portefeuille relativement au marché.

En d’autres mots, il s’agit d’une mesure de covariance d’un portefeuille avec le marché dans son ensemble (de manière typique le S&P 500, ou tout autre point de référence que l’on jugera adapté).

Par exemple, pour un bêta de 2 sur une période donnée, le portefeuille en question aura fluctué de 2 %. Le marché dans son ensemble aura fluctué de 1 %.